并行与分布式计算作业2

姓名	学号	班级	邮箱
张景润	18340210	计科八班	zhangjr35@mail2.sysu.edu.cn

第一题

题目

分别采用不同的算法（非分布式算法）例如一般算法、分治算法和Strassen算法等计算计算矩阵两个300x300的矩阵乘积，并通过Perf工具分别观察cache miss、CPI、 mem_load 等性能指标。

解答

一般算法

编写一个矩阵乘法程序，代码如下:

#include<bits/stdc++.h>
#define SIZE_OF_MATRIX 300
using namespace std;
struct matrix{
  int n,m;
  vector<vector<double> > vec;
  matrix(int nn=0,int mm=0):n(nn),m(mm){
    vec=vector<vector<double> > (n);
    for(int i=0;i<n;i++)vec[i]=vector<double> (m);
  }
  void get_rand(){
    for(int i=0;i<n;i++)for(int j=0;j<m;j++)vec[i][j]=(double)rand()/(INT_MAX);
  }
  void output(){
    for(int i=0;i<n;i++){
      for(int j=0;j<m;j++)cout<<vec[i][j]<<" ";
      cout<<"\n";
    }
  }
  matrix operator *(matrix b){
    if(m!=b.n){
      return matrix();
    }
    matrix ret(n,b.m);
    for(int i=0;i<ret.n;i++){
      for(int j=0;j<ret.m;j++){
        for(int k=0;k<m;k++){
          ret.vec[i][j]+=vec[i][k]*b.vec[k][j];
        }
      }
    }
    return ret;
  }
};
int main(void){
  //cout<<"Hello world\n";
  matrix a(SIZE_OF_MATRIX,SIZE_OF_MATRIX),b(SIZE_OF_MATRIX,SIZE_OF_MATRIX);
  a.get_rand(),b.get_rand();
  //a.output(),b.output();
  
  matrix c=a*b;
  //c.output();
}

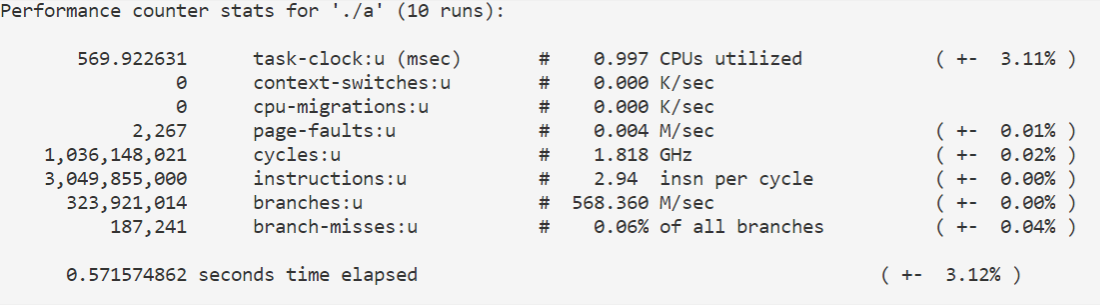
使用perf观察 cache-misses,cpi,mem-loads 等性能指标:

1	perf stat -e cache-misses,instructions,cycles,mem-loads -r 10 ./a

结果如下：

可以看到,10次运行的平均cache-misses次数只有38100次，相比于3e9级别的指令数量，这个数字还是比较少的。
平均指令数为3,373,445,889，平均cpu cycles只有 1,189,821,710，计算得$$CPI=\frac{1,189,821,710}{3,373,445,889}\approx0.3527$$这是一个小于1的数字，十分奇怪，我推测是编译器或者是CPU在底层对循环进行了并行优化。
而mem_loads为0，这也十分奇怪，大概是perf出了什么bug。
用perf record 对cache-misses 和 instructions的分布进行详细分析:

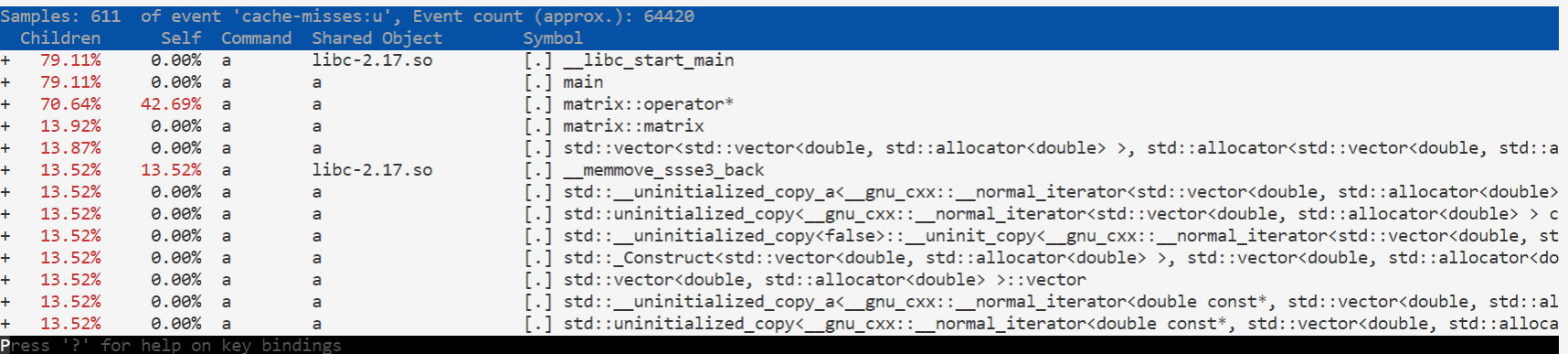
1	perf record -e cache-misses,instructions -g ./a

结果如下：

![57UDL_OJL_`3HPY1F0ND3ZS.png](https://i.loli.net/2020/03/30/Hhj6YGoLQwitACD.png)
可以看到，矩阵乘法阶段占用instructions的比例较高，发生的cache-misses次数也较多。

分治算法

这里的分治算法是利用矩阵分块将矩阵分为4个子矩阵，这样就可以对两个二乘二的矩阵进行乘法，最后再合并起来得到结果。简单的分治算法的时间复杂度仍然是$O(n^3)$的。
代码如下：

#include<bits/stdc++.h>
#define SIZE_OF_MATRIX 300
using namespace std;
const double eps=1e-6;
struct matrix{
  int n,m;
  vector<vector<double> > vec;
  matrix(int nn=0,int mm=0):n(nn),m(mm){
    vec=vector<vector<double> > (n);
    for(int i=0;i<n;i++)vec[i]=vector<double> (m);
  }
  void get_rand(){
    for(int i=0;i<n;i++)for(int j=0;j<m;j++)vec[i][j]=(double)rand()/(INT_MAX);
  }
  void output(){
    for(int i=0;i<n;i++){
      for(int j=0;j<m;j++)cout<<vec[i][j]<<" ";
      cout<<"\n";
    }
  }
  matrix operator *(matrix &b){
    if(m!=b.n){
      return matrix();
    }
    matrix ret(n,b.m);
    for(int i=0;i<ret.n;i++){
      for(int j=0;j<ret.m;j++){
        for(int k=0;k<m;k++){
          ret.vec[i][j]+=vec[i][k]*b.vec[k][j];
        }
      }
    }
    return ret;
  }

  matrix operator+(const matrix& b){
    if(n!=b.n&&m!=b.m){
      return matrix();
    }
    matrix ret(n,m);
    for(int i=0;i<ret.n;i++){
      for(int j=0;j<ret.m;j++){
        ret.vec[i][j]=vec[i][j]+b.vec[i][j];
      }
    }
    return ret;
  }
  
  vector<matrix> divide(){
    matrix m1(n/2,m/2),m2(n/2,m-m/2),m3(n-n/2,m/2),m4(n-n/2,m-m/2);
    for(int i=0;i<m1.n;i++){
      for(int j=0;j<m1.m;j++){
        m1.vec[i][j]=vec[i][j];
      }
    }
    for(int i=0;i<m2.n;i++){
      for(int j=0;j<m2.m;j++){
        m2.vec[i][j]=vec[i][j+m1.m];
      }
    }
    for(int i=0;i<m3.n;i++){
      for(int j=0;j<m3.m;j++){
        m3.vec[i][j]=vec[i+m1.n][j];
      }
    }
    for(int i=0;i<m4.n;i++){
      for(int j=0;j<m4.m;j++){
        m4.vec[i][j]=vec[i+m1.n][j+m1.m];
      }
    }
    return vector<matrix>{m1,m2,m3,m4};
  }


};

  matrix merge(vector<matrix> &matrices){
    matrix ret(matrices[0].n+matrices[3].n,matrices[0].m+matrices[3].m);
    for(int i=0;i<matrices[0].n;i++){
      for(int j=0;j<matrices[0].m;j++){
        ret.vec[i][j]=matrices[0].vec[i][j];
      }
    }
    for(int i=0;i<matrices[1].n;i++){
      for(int j=0;j<matrices[1].m;j++){
        ret.vec[i][j+matrices[0].m]=matrices[1].vec[i][j];
      }
    }
    for(int i=0;i<matrices[2].n;i++){
      for(int j=0;j<matrices[2].m;j++){
        ret.vec[i+matrices[0].n][j]=matrices[2].vec[i][j];
      }
    }
    for(int i=0;i<matrices[3].n;i++){
      for(int j=0;j<matrices[3].m;j++){
        ret.vec[i+matrices[0].n][j+matrices[0].m]=matrices[3].vec[i][j];
      }
    }
    return ret;
  }

  matrix divide_conquer(matrix &a,matrix &b){
    if(a.n<10)return a*b;
    vector<matrix> vec1=a.divide(),vec2=b.divide();
//    cout<<vec1[0].n<<" "<<vec2[3].m<<endl;
    vector<matrix> sub_matrix(4);
    sub_matrix[0]=divide_conquer(vec1[0],vec2[0])+divide_conquer(vec1[1],vec2[2]);
    sub_matrix[1]=divide_conquer(vec1[0],vec2[1])+divide_conquer(vec1[1],vec2[3]);
    sub_matrix[2]=divide_conquer(vec1[2],vec2[0])+divide_conquer(vec1[3],vec2[2]);
    sub_matrix[3]=divide_conquer(vec1[2],vec2[1])+divide_conquer(vec1[3],vec2[3]);
    return merge(sub_matrix);
  }
int main(void){
  //cout<<"Hello world\n";
  matrix a(SIZE_OF_MATRIX,SIZE_OF_MATRIX),b(SIZE_OF_MATRIX,SIZE_OF_MATRIX);
  a.get_rand(),b.get_rand();
  //a.output(),b.output();
  matrix c=divide_conquer(a,b);
  //matrix d=a*b;
  bool ok=true;
  /*for(int i=0;i<SIZE_OF_MATRIX;i++){
    for(int j=0;j<SIZE_OF_MATRIX;j++)if(abs(c.vec[i][j]-d.vec[i][j])>eps)ok=false;//cout<<i<<" "<<j<<" "<<c.vec[i][j]<<" "<<d.vec[i][j]<<endl;
  }
  cout<<ok<<endl;*/
//  c.output();
}

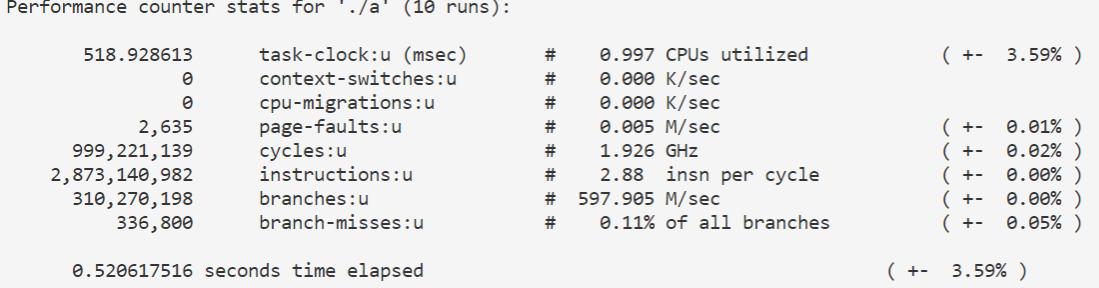
同样是使用

1	perf stat -e cache-misses,instructions,cycles,mem-loads -r 10 ./a

来对性能进行分析，结果如下图所示：

可以看到cache-misses次数与之前基本一样；CPI升高到了0.5208，仍然小于1，说明底层的并行化效果不错；而mem-loads仍然为0。
平均时间消耗达到了将近3秒，是之前的4倍还要多，说明程序在递归调用时消耗了大量时间。

strassen算法

strassen算法用很神奇的方法把矩阵乘法的时间复杂度降低到了$O(n^{2.81})$左右,在矩阵规模较大的情况下性能会更好。
代码如下:

#include<bits/stdc++.h>
#define SIZE_OF_MATRIX 300
using namespace std;
const double eps=1e-6;
struct matrix{
  int n,m;
  vector<vector<double> > vec;
  matrix(int nn=0,int mm=0):n(nn),m(mm){
    vec=vector<vector<double> > (n);
    for(int i=0;i<n;i++)vec[i]=vector<double> (m);
  }
  void get_rand(){
    for(int i=0;i<n;i++)for(int j=0;j<m;j++)vec[i][j]=(double)rand()/(INT_MAX);
  }
  void output(){
    for(int i=0;i<n;i++){
      for(int j=0;j<m;j++)cout<<vec[i][j]<<" ";
      cout<<"\n";
    }
  }
  matrix operator *(const matrix &b)const{
    if(m!=b.n){
      return matrix();
    }
    matrix ret(n,b.m);
    for(int i=0;i<ret.n;i++){
      for(int j=0;j<ret.m;j++){
        for(int k=0;k<m;k++){
          ret.vec[i][j]+=vec[i][k]*b.vec[k][j];
        }
      }
    }
    return ret;
  }

  matrix operator+(const matrix& b)const{
    if(n!=b.n&&m!=b.m){
      return matrix();
    }
    matrix ret(n,m);
    for(int i=0;i<ret.n;i++){
      for(int j=0;j<ret.m;j++){
        ret.vec[i][j]=vec[i][j]+b.vec[i][j];
      }
    }
    return ret;
  }

  matrix operator-(const matrix& b)const{
    if(n!=b.n&&m!=b.m){
      return matrix();
    }
    matrix ret(n,m);
    for(int i=0;i<ret.n;i++){
      for(int j=0;j<ret.m;j++){
        ret.vec[i][j]=vec[i][j]-b.vec[i][j];
      }
    }
    return ret;
  }

  vector<matrix> divide()const{
    matrix m1(n/2,m/2),m2(n/2,m-m/2),m3(n-n/2,m/2),m4(n-n/2,m-m/2);
    for(int i=0;i<m1.n;i++){
      for(int j=0;j<m1.m;j++){
        m1.vec[i][j]=vec[i][j];
      }
    }
    for(int i=0;i<m2.n;i++){
      for(int j=0;j<m2.m;j++){
        m2.vec[i][j]=vec[i][j+m1.m];
      }
    }
    for(int i=0;i<m3.n;i++){
      for(int j=0;j<m3.m;j++){
        m3.vec[i][j]=vec[i+m1.n][j];
      }
    }
    for(int i=0;i<m4.n;i++){
      for(int j=0;j<m4.m;j++){
        m4.vec[i][j]=vec[i+m1.n][j+m1.m];
      }
    }
    return vector<matrix>{m1,m2,m3,m4};
  }


};

  matrix merge(vector<matrix> &matrices){
    matrix ret(matrices[0].n+matrices[3].n,matrices[0].m+matrices[3].m);
    for(int i=0;i<matrices[0].n;i++){
      for(int j=0;j<matrices[0].m;j++){
        ret.vec[i][j]=matrices[0].vec[i][j];
      }
    }
    for(int i=0;i<matrices[1].n;i++){
      for(int j=0;j<matrices[1].m;j++){
        ret.vec[i][j+matrices[0].m]=matrices[1].vec[i][j];
      }
    }
    for(int i=0;i<matrices[2].n;i++){
      for(int j=0;j<matrices[2].m;j++){
        ret.vec[i+matrices[0].n][j]=matrices[2].vec[i][j];
      }
    }
    for(int i=0;i<matrices[3].n;i++){
      for(int j=0;j<matrices[3].m;j++){
        ret.vec[i+matrices[0].n][j+matrices[0].m]=matrices[3].vec[i][j];
      }
    }
    return ret;
  }

  matrix strassen(matrix a,matrix b){
    if(a.n<=75)return a*b;
    if(a.n&1){
      a.vec.push_back(vector<double>(a.m));
      b.vec.push_back(vector<double>(b.m));
      a.n++,b.n++;
    }
    if(a.m&1){
      for(auto i:a.vec)i.push_back(0);
      for(auto i:b.vec)i.push_back(0);
      a.m++,b.m++;
    }
//    cout<<a.n<<" "<<a.m<<" "<<b.n<<" "<<b.m;
    vector<matrix> vec1=a.divide(),vec2=b.divide();
//    cout<<vec1[0].n<<" "<<vec2[3].m<<endl;
    vector<matrix> m(7);
    m[0]=strassen((vec1[0]+vec1[3]),(vec2[0]+vec2[3]));
    m[1]=strassen((vec1[2]+vec1[3]),vec2[0]);
    m[2]=strassen(vec1[0],(vec2[1]-vec2[3]));
    m[3]=strassen(vec1[3],(vec2[2]-vec2[0]));
    m[4]=strassen((vec1[0]+vec1[1]),vec2[3]);
    m[5]=strassen((vec1[2]-vec1[0]),(vec2[0]+vec2[1]));
    m[6]=strassen((vec1[1]-vec1[3]),(vec2[2]+vec2[3]));
    vector<matrix> mm({m[0]+m[3]-m[4]+m[6],m[2]+m[4],m[1]+m[3],m[0]+m[2]-m[1]+m[5]});
    return merge(mm);
  }
int main(void){
  //cout<<"Hello world\n";
  matrix a(SIZE_OF_MATRIX,SIZE_OF_MATRIX),b(SIZE_OF_MATRIX,SIZE_OF_MATRIX);
  a.get_rand(),b.get_rand();
  //a.output(),b.output();
  
  matrix c=strassen(a,b);
  /*matrix d=a*b;
  bool ok=true;
  for(int i=0;i<SIZE_OF_MATRIX;i++){
    for(int j=0;j<SIZE_OF_MATRIX;j++)if(abs(c.vec[i][j]-d.vec[i][j])>eps)ok=false,cout<<i<<" "<<j<<" "<<c.vec[i][j]<<" "<<d.vec[i][j]<<endl;
  }*/
//  c.output();
}

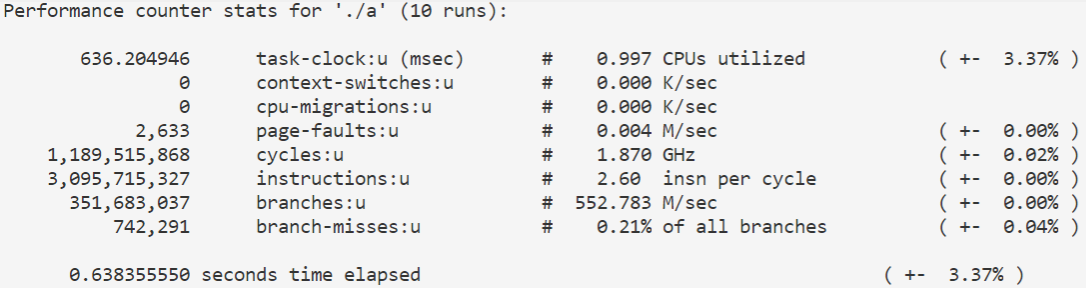
考虑到函数调用会产生大量性能损失，我在strassen函数里设置了一个常量，当矩阵大小小于等于这个量时使用普通的矩阵乘法。
对这个常量值为40,75,150(对应进行三层递归，两层递归，一层递归)分别进行了测试，运行效果如下：

实验证明，进行两层递归的效果最好，为0.52秒左右，比直接计算有稍微的提高。
同样是使用

1	perf stat -e cache-misses,instructions,cycles,mem-loads -r 10 ./a

来对性能进行分析，结果如下图所示：

cache-misses次数较多，CPI是0.347，比之前有所降低。

第二题

本来是打算做一下的，但没装双系统，只有一个linux服务器，又没有管理员权限，只能放弃了。

第三题

题目

Consider a memory system with a level 1 cache of 32 KB and DRAM of 512 MB with the processor operating at 1 GHz. The latency to L1 cache is one cycle and the latency to DRAM is 100 cycles. In each memory cycle, the processor fetches four words (cache line size is four words). What is the peak achievable performance of a dot product of two vectors? Note: Where necessary, assume an optimal cache placement policy.

1 2	for (i = 0; i < dim; i++) dot_prod += a[i] * b[i];

解答

在这里我假设数组的元素都是4字节的float类型，一个word是4个字节，cache分配时不会把上一次刚分配的块覆盖掉，i,dot_prod两个变量放在寄存器里。
则对每一次循环：
①如果i%4==0，则读取a[i]时需要从内存中取出a[i],a[i+1],a[i+2],a[i+3]放在cache里，需要100ns，读取b[i]时需要从内存中取出b[i],b[i+1],b[i+2],b[i+3]放在cache里，需要100ns。则这次循环需要 100ns+100ns+4ns(比较i与dim要1ns,i++要1ns,a[i]b[i]要1ns，将结果加到dot_prod要1ns)，共204ns。
②如果i%4！=0，则a[i],b[i]可以从cache里取出，需要2ns。则这次循环需要 2ns+2ns+4ns，共8ns。
所以，每次循环平均需要 $\frac{38+204}{4}=57ns$故每秒钟能进行17.5M次循环。考虑到每次循环是进行了两次浮点数运算，所以能达到的最高性能是35MFLOPS

第四题

题目

Now consider the problem of multiplying a dense matrix with a vector using a two-loop dot-product formulation. The matrix is of dimension 4K x 4K. (Each row of the matrix takes 16 KB of storage.) What is the peak achievable performance of this technique using a twoloop dot-product based matrix-vector product.

1
2
3

for (i = 0; i < dim; i++)
for (j = 0; j < dim; j++)
c[i] += a[i][j] * b[j];

解答

我们仍然假设cache不会把刚刚分配的块覆盖掉，在取a[i][j]时只需访问一次内存\cache，i和j两个变量放在寄存器里，且i<dim，i++这两个操作可以忽略不计。值得注意的是cache的大小为32k，而b数组大小为16k，矩阵a的一行也是16k，如果cache分配策略是最优的，则b数组会在i=0时全部装进cache里，只有a数组需要重复取出，所以在内存里取出b数组的时间也可以忽略。
则对每一次循环：
①如果j%4==0，则读取a[i][j]时需要从内存中取出a[i][j],a[i][j+1],a[i][j+2],a[i][j+3]放在cache里，需要100ns。c[i]只有一开始会从内存中取到cache里(这一次的用时也忽略不计)，之后一直在寄存器里放着。
则这次循环需要 100ns+5ns(假设比较j与dim要1ns,j++要1ns,a[i][j]b[j]要1ns，取出c[i]要2ns，将结果加到c[i]要1ns)，共106ns。
②如果i%4！=0，则a[i][j],b[j]可以从cache里取出，需要2ns。则这次循环需要 2ns+2ns+6ns，共10ns。
所以，每次循环平均需要 $\frac{310+106}{4}=34ns$,每秒钟能执行29.4M次循环，能达到的最高性能是59.8MFLOPS。

总结

这次实验还是很有难度的。使用perf需要在linux系统，而我只有一个WSL,用不了perf，于是只能找人借了个linux服务器账号。好不容易完成了第一问，去钻研第二问的时候又遇到了很多不会的知识。折腾一番后总算明白要用到linux内核，但我没有管理员权限，用不了，只得作罢。虽然没能把第二问做出来，但多多少少还是有点收获。
做到后面的时候发现第一问的矩阵乘法还有很多可以优化的地方，如vector改为数组、把数组改为指针等，但时间有限就没有修改了。