0%

时间序列相似度

发表于

时间序列相似度度量标准实现

预备知识：样本相似度度量标准

基础类型

距离型

以差值为基础的相似度计算方法，通常值越小越相似。

例子1： 欧式距离

假设时间序列 $X={x_1,x_2……x_n}，Y={y_1,y_2……y_n}$，则可以定义它们之间的欧式距离：

$d_{L^p}=(\sum\limits_{k=1}^{n}\left\vert x_k-y_k \right\vert^p)^{\frac 1p}$

当 $p=1$ 时，距离为 $d_{L^1}=(\sum\limits_{k=1}^{n}\left\vert x_k-y_k \right\vert)$，也称为曼哈顿距离。

当 $p=2$ 时，距离为 $d_{L^2}=(\sum\limits_{k=1}^{n}\left\vert x_k-y_k \right\vert^2)^{\frac 12}$，也称为欧几里得距离

当 $p\rightarrow \infin$ 时，距离为 $d_{L^\infin}=\max\limits_{1\le k \le n}\left\vert x_k-y_k \right\vert$

例子2：马氏距离（可以看成欧式距离使用协方差矩阵达成的标准化形式）

两个向量的马氏距离为：

$$d(\vec x,\vec y)=\sqrt{(\vec x-\vec y)^{T}\sum^{-1}(\vec x-\vec y)}$$

其中，$\sum$ 为 $\vec x$ 和 $\vec y$ 的协方差矩阵。

为什么要用马氏距离？欧式距离不行吗？考虑下面这个例子：

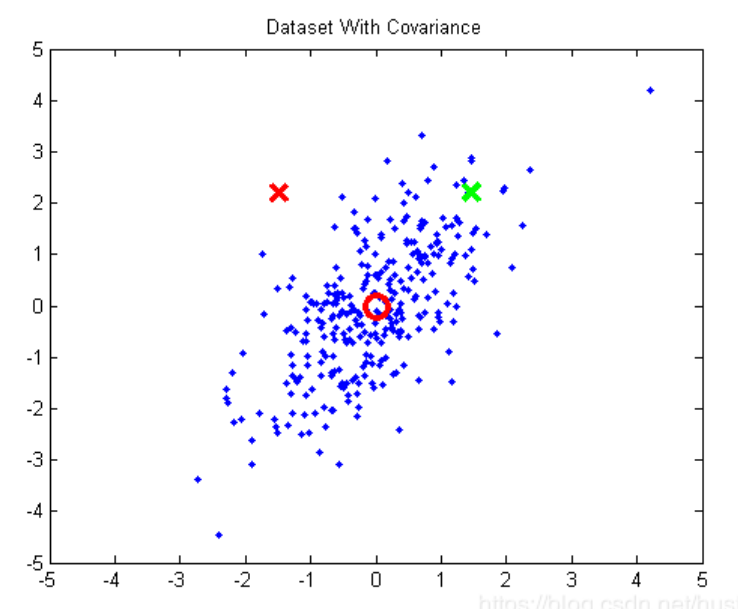
image-20200602210843484.png

上图中，红圆圈是数据点的均值，绿色的×和红色的×到均值的欧式距离是相等的，但我们可以明显地看到，绿色的×应该属于这个分布，红色的×不属于。这是因为

  1. 不同维度(x轴，y轴)之间存在相关性(在这里表现为x轴与y轴存在正相关)。

  2. 不同方向上变化幅度不同，把图顺时针旋转45度，可以看到横向上变化较大，竖向上变化较小(有些资料把这一点称为量纲不同和方差不同)。

用马氏距离就可以消除这种差别，它相当于把欧式距离进行了标准化。

夹角型

以乘积为基础的相似度计算方法，通常值越大越相似。可以通过取相反数达成值越小越相似。

例子1：夹角余弦

假设时间序列 $X={x_1,x_2……x_n}，Y={y_1,y_2……y_n}$，则可以定义它们之间的夹角 $\theta$ 满足：

$cos\theta=\frac{\sum\limits_{k=1}^{n}x_ky_k}{\sqrt{\sum\limits_{k=1}^{n}x_k^2}\sqrt{\sum\limits_{k=1}^{n}y_k^2}}$

例子2：相关系数（其实也可以看成夹角余弦通过每个特征减均值达成的标准化形式）

假设时间序列 $X={x_1,x_2……x_n}，Y={y_1,y_2……y_n}$，则可以定义它们之间的Pearson相关系数 $cor(X,Y)$ 满足：

$cor(X,Y)=\frac{\sum\limits_{k=1}^{n}(x_k-\bar x)(y_k-\bar y)}{\sqrt{\sum\limits_{k=1}^{n}(x_k-\bar x)^2}\sqrt{\sum\limits_{k=1}^{n}(x_k-\bar x)^2}}$

针对特殊结构数据

时间序列

核心需要：对齐

什么是对齐：样本特征的互相配对。

为什么要对齐：样本的相似度是根据样本特征的相似度累加/平均的，结构化数据的特征直接对齐了，但时间序列的每一时刻值可能没有天然强对齐关系。

得到样本相似度度量的实际处理：不同对齐策略下的相似度度量最值

不同对齐策略指对对齐的搜索空间的不同约束，搜索空间的大小会导致不同的复杂度。

时间序列对齐策略的潜在需求：

保序性（单调性）：例如T1:a, b, c; T2:x, y, z，无论怎么配对，T1配对出的匹配序列T2‘顺序满足y不会在x前面，z不会再x,y前面。

保端点型对齐策略

可以一对多，需要全部点（时间序列各个时刻的值）都找到配对（从而开始点一定配对开始点，结束点一定配对结束点，也满足连续性）

比较适合的场景：语音相似度识别

典型例子：DTW（[Dynamic Time Warping，动态时间规整）：保端点型对齐策略下的距离型度量

img

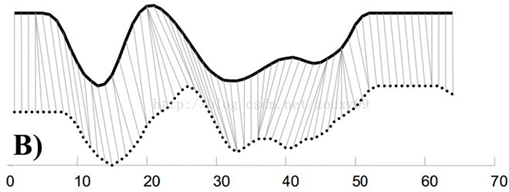
上图就是DTW对齐策略的一个例子。

最基本的DTW可以用动态规划(dp)来实现。具体的，假设时间序列 $X={x_1,x_2……x_m}，Y={y_1,y_2……y_n}$ ，用 $dp[i][j] ,i\le m,j\le n$ 来表示 $X$ 的前 $i$ 个点和 $Y$ 的前 $j$ 个点能取得的最小距离，定义状态转移方程为：

​ $$dp[i][j]=\begin{cases} dist(1,1),i=1,j=1 \ dp[i-1][j]+dist(i,1)，i>1,j=1 \ dp[i][j-1]+dist(1,j),i=1,j>1\min(dp[i-1][j-1],dp[i][j-1],dp[i-1][j-1])+dist(i,j),i>1,j>1 \end{cases}$$

其中 $dist(i,j)=(X[i]-Y[j])^2$ 。

为了将结果可视化，可以将距离矩阵（即 dist ）绘制出来，如 $X=[3,6,8],Y=[2,4,8,7]$ 时，距离矩阵如下所示：

image-20200604221146644.png

要达到一个最小距离，相当于从左上角走到右下角，且每次只允许往右、往下或者往右下走，使得走过的数字的和最小。显然在这个图里应该这样走：

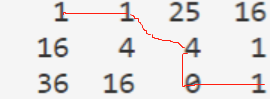
image-20200604221539941.png

DTW的优点

DTW能处理长度不同的时间序列，这是它比传统的距离算法强的地方。而且对很多时间序列，用DTW进行距离计算明显更合理。

DTW的缺点

用距离来度量相似度的算法的时间复杂度是 $O(n)$ ，空间复杂度是 $O(1)$ 的 ，而DTW算法在时间和空间上都是 $O(nm)$ 的。对于较长的时间序列，直接进行计算显然开销太大，于是要引进一些优化的方法。

以下的变种是基于缩减搜索空间得到的变种。

DTW变种1：greedy-DTW

来自论文《Time2Graph: Revisiting Time Series Modeling with Dynamic Shapelets》的附录A.1的Algorithm 5

这种算法是用贪心的思想，即每次选择所有能走的点里代价最小的点。为了避免出现沿着边缘走的情况，设置一个窗口 $w$ ，规定走到的位置 $x,y$ 满足 $|x-y|\le w$ 。比如说，对时间序列 $X=[2,3,5,7,1],Y=[4,2,8,6,4]$，dist矩阵和走过的路线是这样子的：

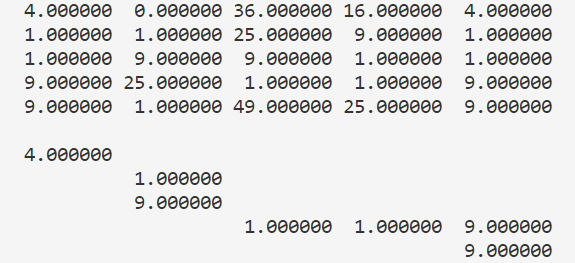
image-20200605171339497.png

greedy-DTW的优点

它最大的优点是速度快，只需要 $O(n+m)$ 的时间复杂度就可以完成计算。

greedy-DTW的缺点

缺点也很明显，贪心算法无法保证取得全局最优解，容易”误入歧途”。

DTW变种2：Fast-DTW

来自论文《FastDTW: Toward Accurate Dynamic Time Warping in Linear Time and Space》

可参考https://www.cnblogs.com/kemaswill/archive/2013/04/18/3029078.html

这种方法的基本策略是递归。FastDTW 算法如下：

对于两个时间序列 $X=[1,2,3,4],Y=[3,4,5,6]$，首先将它们的长度缩短为一半，变成 $X’=[1.5,3.5],Y’=[3.5,5.5]$ ，相对应的，矩阵从 4×4 变成了 2×2，如下图所示：

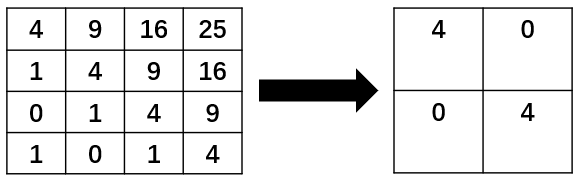
image-20200606011018301.png

然后，对压缩后的时间序列递归地应用 FastDTW找到一条路径（由于这里的时间序列长度只有2，就可以直接找到不用递归），如下所示：

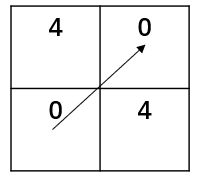
image-20200606011233288.png

在原来的矩阵中给这条路径经过的块打上标记，如下所示：

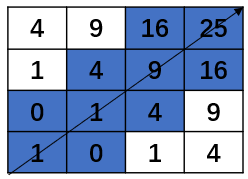
image-20200606011749696.png

为了增大搜索范围，对路径以 $r$ 为半径拓展，即将与路径的距离小于等于 $r$ 的路径打上标记。$r=1$ 时，如下所示：

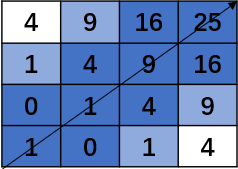
image-20200606012002821.png

这样，就得到了我们的搜索路径，然后只用在这条路径里找就可以了。看起来，搜索路径并不比原来的矩阵小多少，但当时间序列长度足够大时，搜索路径会很小，因为它是 $O(n*r)$ 的，证明略。

Fast-DTW的优点

最大的优点显然是速度快，如下图所示（顺便吐槽一句，04年的时候执行一个 $n=1000$ 的 $O(n^2)$ 算法竟然要0.92秒，而今天的计算机可能不用0.01秒，看来计算机领域的发展还是很快的）：

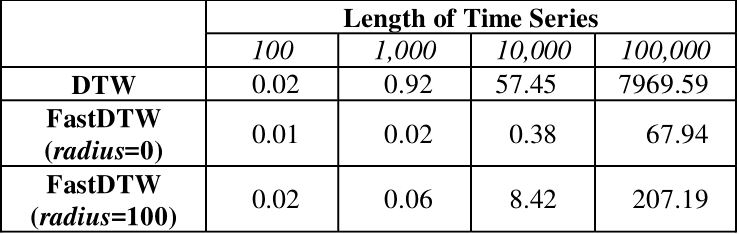
image-20200606012512919.png

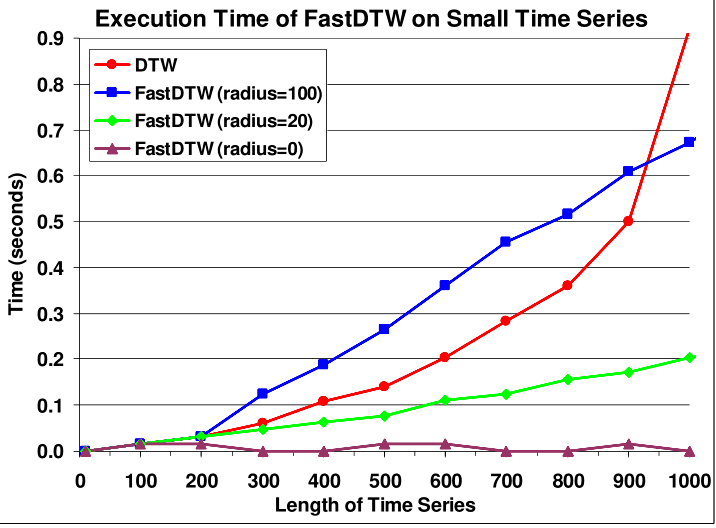
image-20200606012619988.png

对于 $N=1000$ 左右的时间序列，用 $r=20$ 的 Fast-DTW 会比 DTW 快了 4-5倍。当 $N$ 不断增大时，加速效果还会更明显。

Fast-DTW的缺点

由于这种方法得到的是较优解，因此我们有必要关注它的误差。定义误差如下所示：

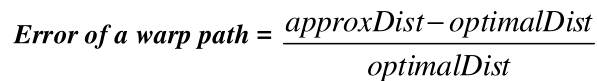
image-20200606013024726.png

经过试验得到误差大小：

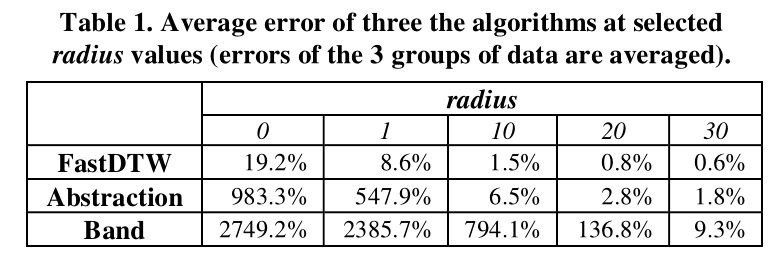
image-20200606013005315.png

可以看到，当 $r=20$ 时，平均误差已经小于 $1%$ 。虽然误差仍然存在，但已经基本可以忽略。

还有一个缺点是编程难度较DTW大。

DTW变种3：constrained DTW

来自论文《Searching and mining trillions of time series subsequences under dynamic time warping》

这篇文章对几种已有的剪枝策略进行了讨论，对它们的下界和时间复杂度进行了比较进行了比较，如下图所示：

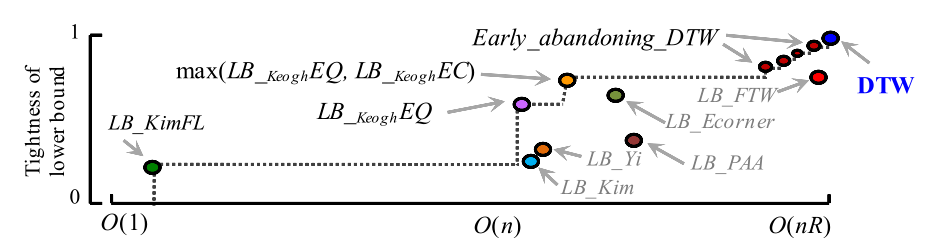
image-20200606141816713.png

一般认为在虚线下方的剪枝策略是没用的，因为至少存在一种下界更高且时间复杂度更低的策略。

最终作者决定用这种策略：先用 $LB_{Kim}FL$ ，如果不能大于 $Best_so_far$ ，则再用 $LB_{Keogh}EQ$ ，还是不行就用 $LB_{Keogh}EC$，再不行就用 $Early_abandoning_DTW$ 。

至于cDTW，似乎这篇论文并没有提到，查了其他的资料，大概就是把DTW的路径限制在对角线旁边的样子。

平移型对齐策略

只可一对一，允许两边边界的点（端点及端点附近点）找不到配对，满足连续性。

比较适合的场景：时钟不共享而有一定偏差的两条时间序列

典型例子：cross-correlation：平移型对齐策略下的夹角型度量

可参考论文<<k-Shape: Efficient and Accurate Clustering of Time Series>>的3.1节的介绍

cross-correlation的定义与卷积类似，对于函数 $f(x)$ 和 $g(x)$ ，它们的 cross-correlation 定义为

$$h(x)=\int_{-\infin}^{+\infin}f(t)g(x+t)dt$$。事实上，把 + 号改为 - 号就是卷积了。两个已经标准化了的时间序列 $\vec x=(x_1,…,x_m)$ 和 $\vec y=(y_1,…,y_m)$ 的 cross-correlation 可以这样定义：$CC(\vec x,\vec y)=(c_1,c_2,…,c_{2*m-1})$

其中：$c_{k+m}=\begin{cases}\sum\limits_{l=1}^{m-k}x_{l+k}y_l,k>0\ \vec x · \vec y ,k=0 \ \sum\limits_{l=1-k}^{m}x_{l+k}y_l,k<0 \end{cases}$

然后在 $CC(\vec x,\vec y)$ 中找到一个最大的，记为 $CC_w(\vec x,\vec y)$，定义 $NCC_c(\vec x,\vec y)=\frac{CC_w(\vec x,\vec y)}{\sqrt{R_0(\vec x,\vec x)·R_0(\vec y,\vec y)}}$。这样就把距离归化到 $[-1,1]$。再定义 $SBD(\vec x,\vec y)=1-NCC_c(\vec x,\vec y)$ ，则得到 向量 $\vec x$ 和向量 $\vec y$ 的 SBD（Shape-based distance）距离，对于形状接近的时间序列，这个值接近于0，否则接近于2。

值得注意的是，直接计算两个长为 $m$ 的时间序列的SBD距离是 $O(m^2)$ 的，但我们知道两个序列的卷积可以 $O(mlogm)$ 地计算，而)卷积只用把 $\vec x$ 翻转一下就变成了 $CC(\vec x,\vec y)$，因此，计算 SBD 距离也是 $O(mlogm)$ 的。这会比 $O(m^2)$ 的 DTW 算法快很多。

以下的变种是基于不同标准化思路得到的变种。

<<k-Shape: Efficient and Accurate Clustering of Time Series>>的3.1节的公式8的3个变种

定义 $NCC_b(\vec x,\vec y)=\frac{CC_w(\vec x,\vec y)}{m}$ 这样的结果并不会归一化到一个区间，有啥规律我也看不出来…

定义 $NCC_u(\vec x,\vec y)=\frac{CC_w(\vec x,\vec y)}{w-|w-m|}$，这样的结果是上面有多少项相乘，则结果就除以多少。